Robots
COMPAS provides several fundamental structures and features that simplify working with robots models, kinematic chains and coordinate frames. On top of this, the COMPAS FAB extension package provides additional functionality to connect these models with planning and execution tools and libraries.
Coordinate frames
One of the most basic concepts related to robotics that COMPAS provides are
coordinate frames, which are described using the compas.geometry.Frame class.
In any robotic setup, there exist multiple coordinate frames, and each one is defined in relation to the next. Examples of typical coordinate frames are:
World coordinate frame (
WCF)Robot coordinate frame (
RCF)Tool0 coordinate frame (
T0CF)Tool coordinate frame (
TCF)Object coordinate frame (
OCF)
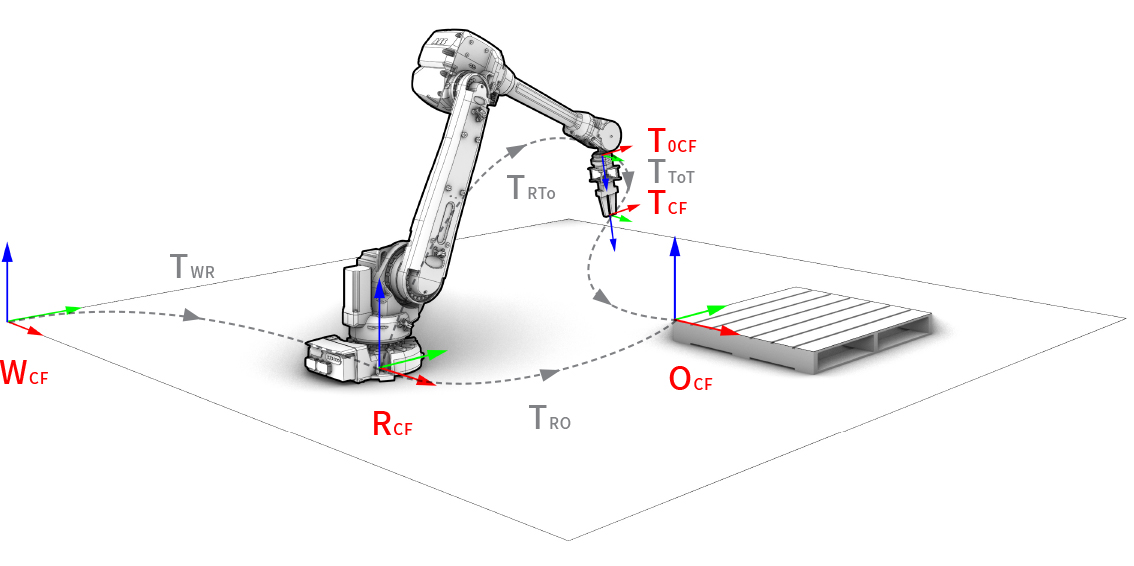
Coordinate frame convention of a robotic setup.
A coordinate frame is defined as a point and two orthonormal base vectors
(xaxis, yaxis). Both the point and the vectors can be defined
using simple lists of XYZ components or using classes. Frames are
right-handed coordinate systems. The following two examples are equivalent:
>>> from compas.geometry import Frame, Point, Vector
>>> frame = Frame([0, 0, 0], [1, 0, 0], [0, 1, 0])
>>> frame.point
Point(0.000, 0.000, 0.000)
>>> frame = Frame(Point(0, 0, 0), Vector(1, 0, 0), Vector(0, 1, 0))
>>> frame.point
Point(0.000, 0.000, 0.000)
There are shorthand constructors for the frames located at (0.0, 0.0, 0.0):
>>> f1 = Frame.worldXY()
>>> f2 = Frame.worldYZ()
>>> f3 = Frame.worldZX()
And there are additional constructors to create coordinate frames from alternative representations such as:
>>> f4 = Frame.from_axis_angle_vector([0, 0, 0], point=[0, 0, 0])
>>> f5 = Frame.from_points([0, 0, 0], [1, 0, 0], [0, 1, 0])
>>> f6 = Frame.from_quaternion([1, 0, 0, 0], point=[0, 0, 0])
The relationship between coordinate frames is expressed as a
compas.geometry.Transformation between the two, for example:
>>> from compas.geometry import Transformation
>>> f1 = Frame([15, 15, 15], [0, 1, 0], [0, 0, 1])
>>> f2 = Frame.worldXY()
>>> t = Transformation.from_frame_to_frame(f1, f2)
Transformation([[0.0, 1.0, 0.0, -15.0], [0.0, 0.0, 1.0, -15.0], [1.0, 0.0, 0.0, -15.0], [0.0, 0.0, 0.0, 1.0]])
A very common need is to describe the position and rotation of a object
(eg. point, vector, mesh, etc.) in relation to its local coordinate frame,
and then transform it to the world coordinate frame, and vice versa.
These operations are simplified with the methods to_local_coordinates
and to_world_coordinates of frames:
>>> f1 = Frame([130, 25, 80], [1, 0, 0], [0, 1, 0])
>>> local_point = Point(10, 10, 10)
>>> f1.to_world_coordinates(local_point)
Point(140.000, 35.000, 90.000)
Conversely, an object defined in world coordinate frame can be transformed to
a local coordinate frame using the to_local_coordinates method:
>>> p = Point(10, 10, 10)
>>> f1 = Frame([130, 25, 80], [1, 0, 0], [0, 1, 0])
>>> f1.to_local_coordinates(p)
Point(-120.000, -15.000, -70.000)
Robot models
Robotic arms, like those typically used in digital fabrication, are fundamentally kinematic chains of rigid bodies, i.e. links, connected by joints to provide constrained motion. Kinematics is a subdomain of mechanics, and contrary to dynamics, it concerns the laws of motion without considering forces.
A robot model is a set of links and joints that form a tree structure where each joint has a coordinate frame around which it rotates or translates, depending on the joint type.
COMPAS supports robot models defined in a standard robot description format
called URDF, which originates in the ROS community.
Links
Links are the rigid bodies in a robot model. They can have zero or more geometries associated. Associated geometry can serve visual or collision purposes. Collision geometry is generally a simplified version of visual geometry to speed up the collision checking process.
Joints
Joints are the connecting elements between links. There are four main types of joints:
Revolute: A hinge joint that rotates along the axis and has a limited range specified by the upper and lower limits.
Continuous: A hinge joint that rotates along the axis and has no limits.
Prismatic: A sliding joint that slides along the axis, and has a limited range specified by the upper and lower limits.
Fixed: Not really a joint because it cannot move, all degrees of freedom are locked.
Visualizing Robots
Before jumping into how to build a robot model, let’s first see how to visualize one. This can be done with Blender, Rhino or Grasshopper using one of COMPAS’s artists. The basic procedure is the same in any of the CAD software (aside from the import statement). Below you can find an example code for both Rhino and Blender.
Be sure to first install COMPAS for Rhino. While the following code is incomplete, it can be used as a scaffolding for code to be run in a Python script editor within Rhino.
import compas
from compas.artists import Artist
from compas.robots import RobotModel
model = RobotModel('Robby')
# Add some geometry to Robby here
artist = Artist(model, layer='COMPAS::Example Robot')
artist.clear_layer()
artist.draw_visual()
import compas
from compas.artists import Artist
from compas.robots import RobotModel
import compas_blender
compas_blender.clear() # Delete all objects in the Blender scene
model = RobotModel('Robby')
# Add some geometry to Robby here
# Load the robot geometry into the blender scene
artist = Artist(model, collection='COMPAS::Example Robot')
See below for a complete example of how to programmatically create a Robotmodel.
Building robots models
Robot models are represented by the compas.robots.RobotModel class.
There are various ways to construct a robot model. The following snippet
shows how to construct one programmatically:
>>> from compas.robots import Joint, Link, RobotModel
>>> j1 = Joint('joint_1', 'revolute', parent='base', child='link_1')
>>> j2 = Joint('joint_2', 'revolute', parent='link_1', child='link_2')
>>> j3 = Joint('joint_3', 'revolute', parent='link_2', child='link_3')
>>> j4 = Joint('joint_4', 'revolute', parent='link_3', child='link_4')
>>> j5 = Joint('joint_5', 'revolute', parent='link_4', child='link_5')
>>> j6 = Joint('joint_6', 'revolute', parent='link_5', child='link_6')
>>> l0 = Link('base')
>>> l1 = Link('link_1')
>>> l2 = Link('link_2')
>>> l3 = Link('link_3')
>>> l4 = Link('link_4')
>>> l5 = Link('link_5')
>>> l6 = Link('link_6')
>>> links = [l0, l1, l2, l3, l4, l5, l6]
>>> joints = [j1, j2, j3, j4, j5, j6]
>>> robot = RobotModel('johnny-5', joints=joints, links=links)
>>> robot.get_configurable_joint_names()
['joint_1', 'joint_2', 'joint_3', 'joint_4', 'joint_5', 'joint_6']
This approach can end up being very verbose, so the methods add_link
and add_joint of compas.robots.RobotModel offer an alternative that
significantly reduces the amount of code required. Starting with an empty
robot model, adding a link in the shape of a box is as easy as:
>>> from compas.geometry import Box, Frame
>>> from compas.robots import RobotModel
>>> model = RobotModel(name='Boxy')
>>> box = Box(Frame.worldXY(), 1, 2, .5)
>>> model.add_link(name='box_link', visual_meshes=[box])
This code snippet can be modified and run in a Rhino python editor
to visualize Boxy. Throughout the rest of this tutorial, the code
snippets will include the lines for visualization in Rhino, but be
aware that the class compas.robots.RobotModel can be used,
and is useful, outside of a CAD environment.
from compas.artists import Artist
from compas.geometry import Box, Frame
from compas.robots import RobotModel
model = RobotModel(name='Boxy')
box = Box(Frame.worldXY(), 1, 2, .5)
model.add_link(name='box_link', visual_meshes=[box])
artist = Artist(model, layer='COMPAS::Example Robot')
artist.clear_layer()
artist.draw_visual()

As can be seen, this has added a box of dimensions 1 x 2 x .5
whose geometric center and orientation coincides with the world XY frame.
The visual_meshes argument can be given a list containing COMPAS
primitives such as compas.geometry.Box or the more complex
COMPAS meshes compas.geometry.Mesh. For simplicity,
this tutorial uses only primitives.
To reposition the box relative to the link’s origin, simply change the frame of the provided box. To move the box so that it sits above the XY plane, the origin must be shifted in the z-direction by half the height of the box. The box is also shifted slightly forward in the y-direction:
from compas.artists import Artist
from compas.geometry import Box, Frame
from compas.robots import RobotModel
model = RobotModel(name='Boxy')
box = Box(Frame([0, .5, .25], [1, 0, 0], [0, 1, 0]), 1, 2, .5)
model.add_link(name='box_link', visual_meshes=[box])
artist = Artist(model, layer='COMPAS::Example Robot')
artist.clear_layer()
artist.draw_visual()

A link may have more than one geometric element associated to it. Now there is a stack of two boxes:
from compas.artists import Artist
from compas.geometry import Box, Frame
from compas.robots import RobotModel
model = RobotModel(name='Boxy')
box_1 = Box(Frame([0, .5, .25], [1, 0, 0], [0, 1, 0]), 1, 2, .5)
box_2 = Box(Frame([0, 0, 4], [1, 0, 0], [0, 1, 0]), .5, 1, 7)
model.add_link(name='box_link', visual_meshes=[box_1, box_2])
artist = Artist(model, layer='COMPAS::Example Robot')
artist.clear_layer()
artist.draw_visual()

Remember that the frame of the box is the geometric center of the box relative
to the link’s origin (which, in this case, happens to be the world XY frame).
So to stack the boxes, the center of box_2 must be placed at a height of
<height of box_1> + 1/2 * <height of box_2> = .5 + .5 * 7 = 4.
One link does not an interesting robot make. The following code snippet adds a cylindrical second link as well as a joint connecting the two.
from compas.artists import Artist
from compas.geometry import Box, Circle, Cylinder, Frame, Plane, Vector
from compas.robots import Joint, RobotModel
model = RobotModel(name='Jointy')
box_1 = Box(Frame([2, .5, .25], [1, 0, 0], [0, 1, 0]), 1, 2, .5)
box_2 = Box(Frame([2, 0, 4], [1, 0, 0], [0, 1, 0]), .5, 1, 7)
box_link = model.add_link(name='box_link', visual_meshes=[box_1, box_2])
cylinder = Cylinder(Circle(Plane([0, 0, 0], [0, 0, 1]), .5), 8)
cylinder_link = model.add_link(name='cylinder_link', visual_meshes=[cylinder])
origin = Frame([0, 0, 7], [1, 0, 0], [0, 1, 0])
axis = Vector(1, 0, 0)
model.add_joint(
name='box_cylinder_joint',
type=Joint.CONTINUOUS,
parent_link=box_link,
child_link=cylinder_link,
origin=origin,
axis=axis,
)
artist = Artist(model, layer='COMPAS::Example Robot')
artist.clear_layer()
artist.draw_visual()

There’s a lot going on in this snippet, so let’s break it down. First, the link
containing the stacked boxes is added, but the geometry has been shifted to the
side 2 units in the x-direction. Second, a cylindrical link is added.
The cylinder has height 8 and radius .5 and is vertically oriented. Finally, a
joint is added. This is the most involved operation so far, so let’s explore
this in detail.
Several parameters must be defined for the joint to be sensible.
The required parameters for a minimally defined joint are the name, type,
parent_link and child_link. The location and orientation of the joint is defined
by the origin, which specifies a frame relative to the origin of the parent_link.
In this case, the location of the joint is located 7 units above (ie,
in the z-direction) the origin of the box_link, making it .5 units below the top
of the second box. The origin of the joint also specifies the origin of its
child_link. Here, this means that the center of the cylinder will coincide with
the location of the joint. Since the geometries of the boxes have been shifted,
the boxes and the cylinder do not overlap. If the joint origin is not specified,
it will default to coincide with the origin of the parent_link. Since a continuous
joint was added, it makes sense that the axis of rotation would also need to be given.
Here, the joint will rotate about the joint origin’s x-axis.
Adding a bit more geometry and a few links with fixed joints and we arrive at a rough
model of the classic drinking bird toy (full code
here).

While it can be useful to programmatically create a robot, more often than not, robot
models are loaded from URDF files. To load a URDF into a robot model, use the
from_urdf_file method:
>>> model = RobotModel.from_urdf_file('ur5.urdf')
>>> print(model)
Since a large number of robot models defined in URDF are available on Github, there are specialized loaders that allow loading an entire model including its linked geometry directly from a Github repository:
>>> import compas
>>> from compas.robots import GithubPackageMeshLoader
>>> from compas.robots import RobotModel
>>> # Set high precision to import meshes defined in meters
>>> compas.PRECISION = '12f'
>>> github = GithubPackageMeshLoader('ros-industrial/abb', 'abb_irb6600_support', 'kinetic-devel')
>>> model = RobotModel.from_urdf_file(github.load_urdf('irb6640.urdf'))
>>> model.load_geometry(github)
>>> print(model)
Robot name=abb_irb6640, Links=11, Joints=10 (6 configurable)
Another common scenario is to load robot models from a running ROS system. ROS (Robot Operating System) is a very complex and mature tool, and its setup is beyond the scope of this tutorial, but an overview of some of the installation options is available here. Once ROS is configured on your system, the most convenient way to load the robot model is to use COMPAS FAB and its ROS integration. The following snippet shows how to load the robot model currently active in ROS:
>>> from compas_fab.backends import RosClient
>>> with RosClient() as ros:
... robot = ros.load_robot(load_geometry=True)
... print(robot.model)
FK, IK & Path Planning
Robot models are the base for a large number of additional features that are provided via extension packages. In particular, features such as forward and inverse kinematic solvers and path planning are built on top of these robot models, but are integrated into COMPAS FAB.
For further details about these features, check the detailed examples in COMPAS FAB documentation.